2021年高考全国卷甲卷数学试卷分析

2021-09-22 10:30:01
新学高考

一、命题特点

2021 年四川省高考数学由以往的全国卷Ⅲ变为全国卷甲卷，分文、理两套试卷。2021 年高考数学全国甲卷命题，落实高考内容改革总体要求，贯彻德智体美劳全面发展教育方针，聚焦核心素养，突出关键能力考查，体现了高考数学的科学选拔功能和育人导向。试题突出数学本质，重视理性思维，坚持素养导向、能力为重的命题原则；倡导理论联系实际、学以致用，关注我国社会主义建设和科学技术发展的重要成果，通过设计真实问题情境，体现数学的应用价值；稳步推进改革，科学把握必备知识与关键能力的关系，科学把握数学题型的开放性与数学思维的开放性，稳中求新，体现了基础性、综合性、应用性和创新性的考查要求。

1. 发挥学科特色，彰显教育功能

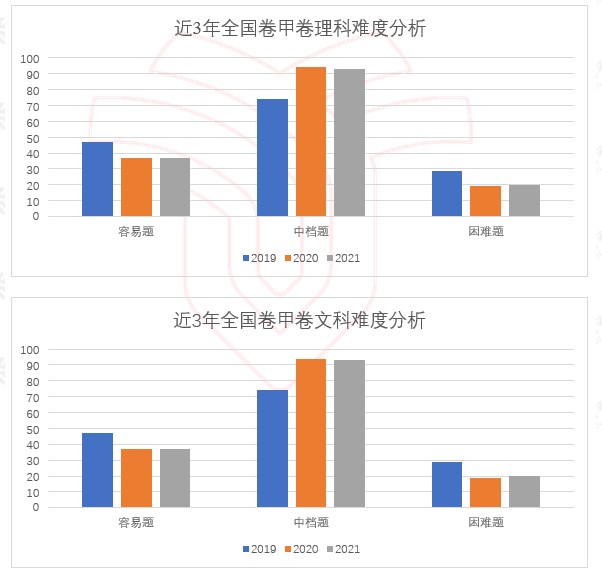
2021 年高考数学全国卷命题，坚持思想性与科学性的高度统一，发挥数学应用广泛、联系实际的学科特点，命制具有教育意义的试题，以增强考生社会责任感，引导考生形成正确的人生观、价值观、世界观。试题运用我国社会主义建设和科技发展的重大成就作为情境，深入挖掘我国社会经济建设和科技发展等方面的学科素材，引导考生关注我国社会现实与经济、科技进步与发展，增强民族自豪感与自信心，增强国家认同，增强理想信念与爱国情怀。一是关注科技发展与进步。比如理科第 8 题以珠穆朗玛峰的高度测量为背

景，考查考生的空间想象能力和阅读理解、数学建模的素养。二是关注社会与经济发展。比如文、理科第 2 题以我国在脱贫攻坚工作取得全面胜利和农村振兴为背景，通过图表给出某地农户家庭收入情况的抽样调查结果，以此设计问题，考查考生分析问题和数据处理的能力。

2. 坚持开放创新，考查关键能力

《深化新时代教育评价改革总体方案》提出，构建引导考生德智体美劳全面发展的考试内容体系，改变相对固化的试题形式，增强试题开放性，减少死记硬背和“机械刷题”现象。2021 年高考数学全国卷命题积极贯彻《总体方案》要求，加大开放题的创新力度，利用开放题考查考生数学学科核心素养和关键能力，发挥数学科的选拔功能。比如理科第 18 题，试题给出部分已知条件，要求考生根据试题要求构建一个命题，充分考查考生对数学本质的理解，引导中学数学在数学概念与数学方法的教学中，重视培养数学核心素养，克服“机械刷题”现象。

3. 倡导理论联系实际，学以致用

2021 年高考数学全国甲卷命题注重理论联系实际，体现数学的应用价值。一是取材真实情境，解决实践问题。新高考Ⅱ卷第 21 题取材于生命科学中的真实问题，考查数学抽象、直观想象、逻辑推理等数学核心素养，体现了基础性、综合性、应用性、创新性的考查要求。甲卷理科第 8 题以测量珠穆朗玛峰高程的方法之一——三角高程测量法为背景设计，要求考生能正确应用线线关系、线面关系、点面关系等几何知识构建计算模型，情境真实，突出理论联系实际。二是关注青少年身心健康。身心健康是素质教育的核心内容，在高考评价体系的核心价值指标体系中，包含有健康情感的指标，要求考生具有健康意识，注重增强体质，健全人格，锻炼意志。2021 年高考数学试题对此也有所体现，如甲卷理科第 4 题（文科第 6 题），以社会普遍关注的青少年视力问题为背景，重点考查考生的数学理解能力和运算求解能力。

总之，2021 年高考数学全国卷试题很好地落实了立德树人、服务选才、引导教学的高考核心功能，同时突出数学学科特色，发挥了高考数学科的选拔功能，对深化中学数学教学改革发挥了积极的导向作用。

二、试题难度

三、试卷结构和题型知识考查分析

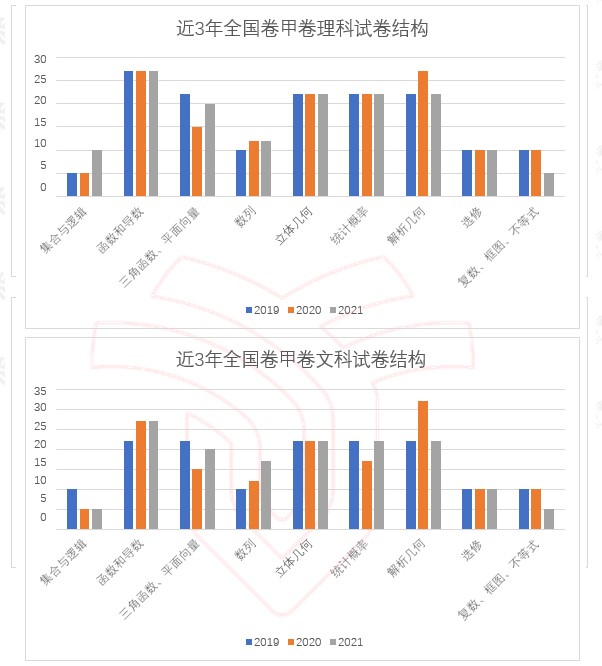
2021 年试卷结构相对稳定，函数和导数，三角函数，数列，立体几何，统计概率，解析几何仍然是高考考察的重点知识板块。

四、下一年的复习思考

1. 学习和研究《考试说明》。《考试说明》是由国家教委考试中心颁发的高考法定性文件,规定了考试的性质、内容、形式等,特别是明确指出了考试内容和考试要求,也就是说要考的知识点及各知识点要考到什么程度均有明确规定。知识要求:指的是数学概念、性质、法则、公式、公理、定理以及其中的数学思想方法。

能力要求:指思维能力、运算能力、空间想象能力以及实践能力和创新意识,大纲对上述能力作了细化说明,并提出了明确的要求。个性品质要求:个性品质是指考生个体的情感、态度和价值观,具有一定的数学视野,认识数学的科学价值和人文价值,崇尚数学的理性精神,形成审慎思维的习惯,体会数学的美学意义。因此,在复习中我们要严格按照《考试说明》中所规定的内容和要求去复习。这样才能做到有的放矢,少走弯路,不故意拨高要求,增强教学的针对性。

2. 钻研课本找标准。其一,现行课本是全国统一的,这不仅仅是内容上的统一,而且定义、定理、公式等叙述上的规范,符号上的使用也是统一的，以课本是标准。其二,许多高考题课本中有原型,即由课本中的例题、习题引伸、变化而来。由此可见脱离课本的复习是不可取的,我们应该以课本为标准,以课本为基础,加强对课本的研究和复习才是根本,特别应将课本中的题目加以引伸、拓宽、变化,做到举一反三,触类旁通，使学生打好基础。

3 研究考题看形式。认真的分析、研究近几年的高考题，比如题目难易程度,考查知识点的情况，预测考试趋势等。要做到心中有数,切实提高复习效率。

4.推敲评价找方向。积极的参加，查阅教委、名校组织举行的高考试题评价会和试题评价报告。通过认真学习、研究、推敲评价报告,我们可以知道许多信息和高考题的改进方向,可从评价报告中找到复习的方向。

五、2021 年高考全国卷甲卷具体考查问题分析

理科数学

题号	板块知识	考查的知识点	难度
1	集合	集合的表达形式，集合的运算：交集	★
2	统计	频率分布直方图，数据分析	★
3	复数	复数运算	★
4	函数	对数运算	★★
5	解析几何	双曲线离心率	★★
6	立体几何	三视图	★★
7	简易逻辑	数列为背景知识，考察充分必要条件	★★★
8	三角函数	立体几何线线、线面关系，结合正余弦定理计算边长	★★★
9	三角函数	三角恒等变换	★★★
10	概率	排列组合	★★★
11	立体几何	外接球问题	★★★
12	函数	函数性质，函数求值	★★★★
13	导函数	求在某点处的切线	★★
14	平面向量	坐标运算，垂直关系	★★
15	解析几何	椭圆的二级结论，焦点三角形的面积	★★★

16	三角函数	已知图形求解析式，求不等式	★★★★
17	统计概率	独立性检验	★★★
18	数列	数列证明	★★★
19	立体几何	证明垂直，求二面角	★★★
20	抛物线	抛物线方程，圆的方程，直线与圆锥曲线的关系	★★★★
21	导函数	求单调性，求交点个数	★★★★★
22	坐标系与参数方程	极坐标方程与直角坐标方程的转换，参数方程	★★★

文科数学

题号	板块知识	考查的知识点	难度
1	集合	集合的表达形式，集合的运算：交集	★
2	统计	频率分布直方图，数据分析	★
3	复数	复数运算	★
4	函数	函数的单调性	★★
5	解析几何	双曲线渐进线，点到直线的距离	★★
6	函数	对数运算	★★
7	立体几何	三视图	★★★
8	三角函数	解三角形，计算边长	★★★
9	数列	等比数列	★★★
10	概率	古典概型	★★★
11	三角函数	三角恒等变换	★★★
12	函数	函数性质，函数求值	★★★★
13	平面向量	向量的模	★★
14	立体几何	圆锥的侧面积	★★
15	三角函数	已知图象求解析式，求值	★★★
16	解析几何	椭圆焦点三角形面积	★★★★
17	统计概率	独立性检验	★★★
18	数列	数列证明	★★★
19	立体几何	求三棱锥体积，证明垂直	★★★
20	导函数	求单调性，求零点问题	★★★★
21	抛物线	抛物线方程，圆的方程，直线与圆锥曲线的关系	★★★★★
22	坐标系与参数方程	极坐标方程与直角坐标方程的转换，参数方程	★★★

六、试卷点评

1.这次的甲卷非常符合“难点分散”的原则，没有极致的难题，但每道题都有卡到学生的地方。压轴题12,16,21题难度相对往年的试卷有所下降，至少思维难度不大。

2.计算量和阅读量较去年有所增加，从第2题开始就需要计算，接着第4、5、8、9都需要计算，第5题考查了双曲线离心率的求法，求解过程中用到了余弦定理，综合性较强，在前6道题出现，对学生有一定挑战；第8题属于三角函数的实际应用问题，体现了高考理论联系实际的要求，题干复杂，阅读量较大，但只要理清条件，结合图形求解即可；9题需要考查三角函数的线切互化，有一定的综合性。16题计算也比较大。

3.反套路意味明显，试题考查的主干知识内容相较前几年变化不大，但是呈现的形式有较大的边化，例如离心率放在了第5题，三角函数以小题考查为主，数列仍然考查大题，并采用了开放设问的形式，引导我们在教学上要重视数学概念的教学，培养核心素养，克服机械刷题。立体几何意外地考查了一个动态问题，如果不能抓住平行的本质第一问的证明会无从下手。解析几何考查了抛物线的切线问题，有着高等数学的背景，如果平时没做过类似问题的学生做对较困难。

4、对于教学的启示：

　　①、大胆猜测今后几年的试题形式和难度可能会波动不定，命题进入“开疆拓土”模式，在总体保持平稳的基础上推陈出新。“核心素养”“能力立意”可能不再是一句空话，怎样培养学生的能力值得更多思考；

　　②、纯靠淘题型做出来的题目比例减少，教学中应更加注重对知识的深层次理解，关注知识的整体结构和内在联系

　　③、高三复习更应个性化，针对不同的学生制定不同的策略，关注学生的考试心态心理以及抗击打的能力。

七、文理卷对比分析

　2021年高考甲卷（文科）主体重视数学基础知识和基本能力，和前两年所不同的是与理科试题不同题数量增多，难度差异较大，具体如下：选择题12个题有7个题不同，其中10、12两个题与理科同题是姊妹题；填空题4个题有3个不同，文科的13和理科的14是从不同方向考的平面向量，文科15和理科16是条件相同要求不同；解答题6个有3个不同：18题数列，理科以开放的形式出的，文理都设成了一题一问的证明；19题立体几何，文理条件相同，要求不同；文科20题和理科21题函数与导数，试题内容不同，要求也不完全相同，文科第一问涉及对参数的讨论（分类讨论）比理科的第一问难，第二问考查方向一样。

　　个人认为文科甲卷总体考得基础，试题大多中规中矩，选填题可以说没有难题，解答题的亮点在18题，此题没按常规，考查等差、等比数列基本量的计算，而是出成了一个证明题，形式不常见，给考场上的考生一定陌生感和压力；20题的第一问分类讨论，学生容易分类不彻底，讨论不全面，导致失分；21题：重在直线与圆之间未知关系的考察，算作比较常规的基本题目，但是计算量较大，多数学生不能完整解决，具有较好的区分度。

　　总体来说此套试卷重视基础，有一定的区分度，可以让学生轻松上手的题目较多，取得满分也不太容易，但在尖子生的筛选上还是缺少点难度。

八、总结陈述

1、坚持立德树人、倡导五育并举

　　如第4题关注青少年视力健康，将指数、对数关系与社会普遍关注的问题相结合，体现体育。

2、坚持实践应用，以数学服务于生活

　　试题坚持与国家的科技社会发展，与人们生活中的实际问题息息相关，如第2题通过概率统计知识解决“我国农村经济收入状况”问题，第17题关注“我国工厂生产”问题，第8题用三角函数知识解决对“珠峰的测量”问题。通过设置真实的问题情境，重点考查学生运用所学知识解决实际问题的能力，数学模型的转化能力，进一步体现了从“解题”到“解决问题”的导向。

3、坚持探索创新，稳步推进高考改革，“结构不良问题”适度开放

　　试题体现鲜明的创新导向，如第18题出现“结构不良的问题”，对试题的创新呈现，突出对学生思维的考查，对数学本质的认识，减少题海战术、机械刷题的效益，引导学生从知识的习得与记忆转向问题的解决、策略的选择，使数学应用发生在思维层面。

4、聚焦主干知识，突出理性思维，考察关键能力

　　根据数学学科特点，重点考查学生的独立思考、逻辑推理及运算、空间想象、数学应用、数学阅读、数学表达等关键能力。对学科的主干知识作为考查重点，如第11题以三棱锥的外接球为背景，侧重空间点线面位置关系及多面体体积的考查，突出考查逻辑推理能力、空间想象能力；第20题解析几何主要考查对方程的同一法的处理，能否找到方程的共同点，从而抽象出方程，使得问题迎刃而解，主要考查学生的观察能力、数学抽象能力、运算求解能力、化归与转化能力；第21题函数与导数主要考查常见的代数变形和（半）分离参数的技巧，最后对过程的表述也是一个重点及难点，此题源于课本。

　　总体而言，试题质量很高、导向性很好。试题突显了数学学科本质，重点是对学生思维的考查、对数学的核心素养和关键能力的考查。也延续了近几年全国卷的基础性、综合性、创新性的特点，没有刻意的为了创新而创新。难度比去年略高，但只要平时认真复习，多注重学科知识和关键能力的培养，考试时再细心、沉稳一点，应该会取得一个比较理想的成绩。

上一篇：2021年普通高等学校招生全国统一考试地理试卷分析（全国甲卷）

下一篇：2021年全国高考甲卷生物部分试题分析